오늘은 수학과 컴퓨터 과학에서 매우 중요한 개념인 '그래프(Graph)'에 대해 자세히 알아보겠습니다.
그래프는 객체들 간의 관계를 나타내는 추상적인 모델로, 네트워크를 구성하는 핵심적인 요소입니다.
이 구조는 데이터 구조와 알고리즘, 복잡한 시스템의 분석에 광범위하게 사용됩니다.
그래프의 기본 개념, 구성 요소, 그리고 다양한 유형과 이들의 활용 방법에 대해 구체적으로 살펴보겠습니다.

1. 노드(정점, Vertex)
그래프의 기본 단위인 노드는 네트워크 내의 개별적인 객체를 나타냅니다. 이는 도시, 컴퓨터, 사람 등 다양한 형태일 수 있습니다.
2. 간선(Edge)
노드들을 연결하는 선으로, 두 객체 사이의 관계를 나타냅니다. 간선은 친구 관계, 도로 연결, 데이터 전송 등을 표현할 수 있습니다.
3. 정점 (Adjacent Vertices)
그래프에서 두 정점이 간선으로 직접 연결되어 있을 때, 이들을 서로 인접해 있다고 합니다.
예를 들어, 그래프에서 정점 A와 정점 B가 직접 연결된 경우, A와 B는 인접 정점입니다.
4. 단순 경로 (Simple Path)
그래프에서 시작 정점에서 끝 정점까지 이어지는 경로 중, 중복되는 정점이 없는 경로를 말합니다.
즉, 같은 정점을 두 번 이상 지나지 않는 경로입니다.
5. 차수 (Degree)
무방향 그래프에서 한 정점에 연결된 간선의 수를 말합니다.
예를 들어, 한 정점에 세 개의 간선이 연결되어 있다면, 그 정점의 차수는 3입니다.
6. 진출 차수 (Outdegree)
방향 그래프에서 특정 정점에서 나가는 간선의 수입니다.
예를 들어, 정점 A에서 다른 정점으로 향하는 간선이 두 개 있다면, A의 진출 차수는 2입니다.
7. 진입 차수 (Indegree)
방향 그래프에서 특정 정점으로 들어오는 간선의 수입니다.
예를 들어, 정점 B로 들어오는 간선이 세 개 있다면, B의 진입 차수는 3입니다.
3. 방향성
방향 그래프(Directed Graph)에서는 간선이 특정 방향을 가리키는 반면, 무방향 그래프(Undirected Graph)에서는 간선이 양방향 관계를 나타냅니다.
4. 가중치(Weight)
간선에 부여된 가중치는 중요도나 비용을 의미하며, 경로 탐색 문제에서 핵심적인 역할을 합니다.
5. 루프와 다중 간선
루프는 같은 노드를 연결하는 간선이고, 다중 간선은 같은 노드 쌍을 여러 번 연결합니다.
그래프 종류
1. 방향 그래프
2. 무방향 그래프
3. 가중치 그래프
4. 사이클 그래프
5. 비순환 그래프
방향그래프

방향 그래프(Directed Graph), 또는 Digraph는 각 간선에 방향이 있는 그래프입니다.
방향 그래프의 간선은 한 정점에서 다른 정점으로의 방향을 나타내며, 일반적으로 화살표로 표시됩니다.
이러한 특성 때문에, 방향 그래프는 간선의 방향이 중요한 상황에서 사용됩니다.
방향 그래프의 주요 특징
1. 방향성
간선은 시작 정점에서 끝 정점으로의 방향을 가집니다. 따라서, 두 정점 A와 B를 연결하는 간선은 A에서 B로 향하는 방향, B에서 A로 향하는 방향, 혹은 둘 다일 수 있습니다.
2. 진입차수와 진출차수
방향 그래프에서는 각 정점에 대해 두 가지 유형의 차수를 고려합니다.
진입차수는 정점으로 들어오는 간선의 수를, 진출차수는 정점에서 나가는 간선의 수를 의미합니다.
3. 비순환성
방향 그래프는 순환(Cycle)을 포함할 수도, 포함하지 않을 수도 있습니다.
특히, 순환을 포함하지 않는 방향 그래프를 방향성 비순환 그래프(Directed Acyclic Graph, DAG)라고 합니다.
4. 응용 분야
방향 그래프는 웹 페이지 간의 링크, 소셜 네트워크에서의 팔로우 관계, 프로젝트 일정 계획, 데이터의 흐름 등 다양한 분야에서 활용됩니다.
무방향 그래프
무방향 그래프(Undirected Graph)는 그래프 이론에서 가장 기본적인 형태의 그래프 중 하나입니다.
이 그래프는 간선에 방향성이 없는 정점들의 집합으로 구성됩니다.
무방향 그래프의 주요특징
1. 간선의 방향성 부재
무방향 그래프의 간선은 방향성을 가지지 않습니다. 즉, 간선은 양쪽 방향으로의 이동을 허용합니다. 예를 들어, 노드 A와 B가 연결된 경우, A에서 B로 또는 B에서 A로 이동할 수 있습니다.
2. 간선 표현
간선은 단순한 선으로 표현되며, 양 끝의 노드를 서로 연결합니다.
3. 차수(Degree)
무방향 그래프에서 한 노드의 차수는 그 노드에 연결된 간선의 수로 정의됩니다. 예를 들어, 한 노드에 세 개의 간선이 연결되어 있다면, 그 노드의 차수는 3입니다.
4. 응용 분야
무방향 그래프는 사회 네트워크에서의 친구 관계, 전기 회로, 도로망 등 방향성이 중요하지 않은 다양한 현실 세계 문제를 모델링하는 데 사용됩니다.
5. 단순 그래프와 다중 그래프
무방향 그래프는 한 쌍의 노드 사이에 최대 한 개의 간선만 허용하는 단순 그래프와, 여러 개의 간선을 허용하는 다중 그래프로 나뉠 수 있습니다.
가중치 그래프
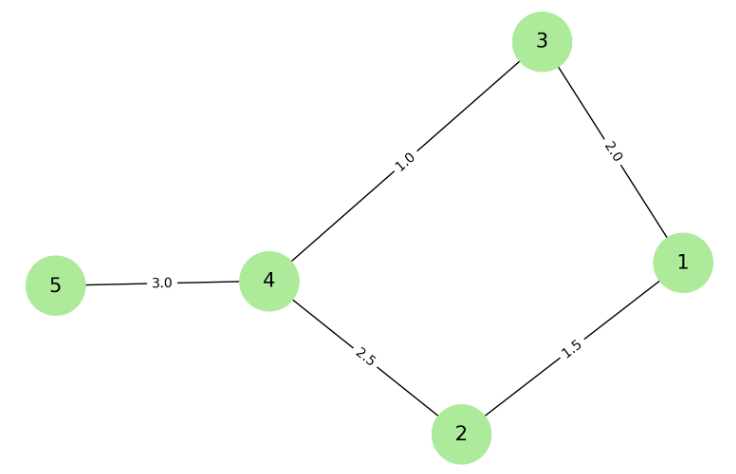
가중치 그래프(Weighted Graph)는 그래프의 간선에 가중치(또는 비용)가 할당된 그래프입니다.
이러한 가중치는 간선의 중요도, 거리, 비용, 시간 등 다양한 수치적 값을 나타낼 수 있으며, 그래프에서의 경로를 평가하는 데 중요한 역할을 합니다.
가중치 그래프는 방향성이 있는 방향 그래프(Directed Graph)와 방향성이 없는 무방향 그래프(Undirected Graph) 모두에 적용될 수 있습니다.
가중치 그래프의 주요 특징
1. 간선의 가중치
각 간선은 특정한 가중치를 가집니다. 이 가중치는 간선이 나타내는 경로의 길이, 비용, 용량 등을 수치화한 것입니다.
2. 응용 분야
가중치 그래프는 실제 세계 문제를 모델링하는 데 널리 사용됩니다. 예를 들어, 도시 간의 거리를 나타내는 도로망, 네트워크 트래픽의 대역폭, 물류 네트워크에서의 운송 비용 등을 표현할 때 사용됩니다.
3. 알고리즘
최단 경로 문제(Dijkstra, Bellman-Ford, Floyd-Warshall 알고리즘 등), 최소 비용 신장 트리(Minimum Spanning Tree, MST) 알고리즘(Kruskal, Prim 알고리즘 등)과 같은 그래프 알고리즘에서 가중치 정보는 매우 중요합니다.
4. 가중치 표현
그래프를 시각화할 때, 간선에 부여된 가중치는 보통 간선 옆에 숫자로 표시되거나 간선의 두께 또는 색상으로 나타낼 수 있습니다.
사이클 그래프
사이클 그래프(Cycle Graph)는 그래프 이론에서 중요한 유형 중 하나로, 모든 노드가 순환적으로 연결된 구조를 가지고 있습니다.
사이클 그래프의 주요 특징
1. 닫힌 루프 형성
사이클 그래프의 모든 노드는 순환적인 경로를 형성하며, 이 경로는 시작 노드로 다시 돌아오는 폐쇄 루프를 만듭니다.
2. 동일한 차수
사이클 그래프의 각 노드는 두 개의 간선으로 연결되어 있으며, 이로 인해 모든 노드의 차수는 동일합니다. 각 노드는 정확히 두 개의 이웃 노드와 연결됩니다.
3. 간단한 구조
사이클 그래프는 가장 간단한 순환 구조를 나타내며, 추가적인 간선이나 복잡한 연결이 없습니다.
4. 응용 분야
사이클 그래프는 순환 회로, 순환적인 네트워크 구조, 또는 어떤 프로세스나 시스템의 반복적인 순환을 모델링하는 데 사용됩니다.
5. 그래프 이론에서의 중요성
사이클 그래프는 그래프 이론에서 기본적인 구조 중 하나로, 많은 이론적 연구와 알고리즘에서 기초적인 역할을 합니다.
비순환 그래프
비순환 그래프는 사이클 그래프를 제외한 그래프입니다.
완전 그래프
완전 그래프(Complete Graph)는 그래프 이론에서 각 노드가 그래프 내의 모든 다른 노드들과 직접 연결된 그래프를 말합니다.
완전 그래프의 주요 특징
1. 노드 간 전체 연결
완전 그래프에서는 모든 노드 쌍이 간선으로 연결됩니다. 이는 그래프 내의 어떤 두 노드도 직접적인 경로로 연결되어 있다는 것을 의미합니다.
2. 간선의 수
N개의 노드를 가진 완전 그래프는 총 N(N-1)/2 개의 간선을 가집니다. 이는 가능한 모든 노드 쌍에 대해 한 개의 간선이 존재한다는 것을 의미합니다.
3. 간단한 구조
완전 그래프는 구조적으로 간단하며, 그래프 이론에서 기본적인 구조 중 하나로 여겨집니다.
4. 응용 분야
완전 그래프는 네트워크 설계, 회로 설계, 컴퓨터 네트워킹 등에서 이론적인 모델로 사용됩니다. 특히, 모든 가능한 연결을 고려해야 하는 최적화 문제에서 중요한 역할을 합니다.
5. 차수(Degree)
N개의 노드를 가진 완전 그래프에서 각 노드의 차수는 항상 N-1입니다. 이는 각 노드가 다른 모든 노드와 연결되어 있다는 것을 의미합니다.
6. 부분 그래프
완전 그래프가 아닌, 그래프는 부분 그래프입니다.
연결 그래프
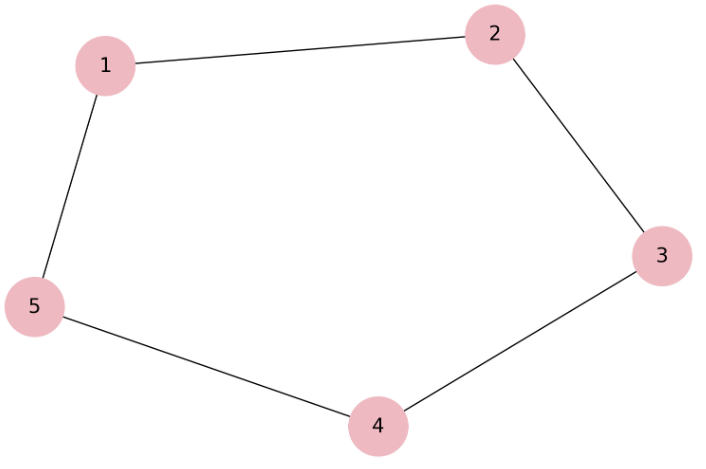
연결 그래프(Connected Graph)는 그래프 이론에서 중요한 개념 중 하나입니다.
연결 그래프는 그래프 내의 모든 노드 쌍이 최소한 하나의 경로를 통해 서로 연결되어 있는 그래프를 말합니다.
즉, 그래프 내의 어떤 노드에서 시작해도 다른 모든 노드로 이동할 수 있습니다.
연결 그래프의 주요 특징
1. 경로의 존재
연결 그래프에서는 그래프 내의 모든 노드 쌍 간에 적어도 하나 이상의 경로가 존재합니다. 이 경로는 직접적일 수도 있고, 여러 노드를 거쳐 이어질 수도 있습니다.
2. 무방향성
연결 그래프는 주로 무방향 그래프를 가리키는 용어로 사용됩니다. 방향 그래프에서는 모든 노드가 서로 연결된 경우에도 '강하게 연결된 그래프(Strongly Connected Graph)'라고 별도로 칭합니다.
3. 트리의 확장형
모든 트리(Tree)는 연결 그래프의 한 예입니다. 트리는 연결 그래프 중에서도 사이클이 없는 특별한 형태를 가집니다.
4. 응용 분야
연결 그래프는 네트워크 설계, 도로망 계획, 사회 네트워크 분석 등 여러 분야에서 활용됩니다. 네트워크가 어떻게 연결되어 있는지를 분석하고 최적화하는 데 중요한 역할을 합니다.
5. 비연결 그래프(Disconnected Graph)
반대로, 그래프 내의 일부 노드 쌍이 서로 연결되지 않은 그래프를 비연결 그래프라고 합니다. 이는 분리된 여러 하위 그래프로 구성될 수 있습니다.
신장 트리(Spanning Tree)
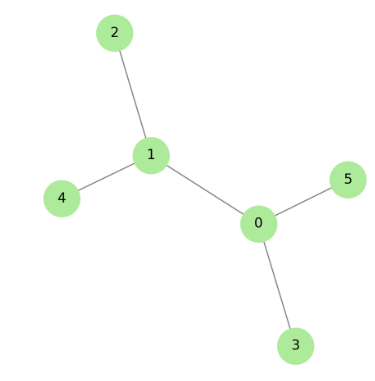
신장 트리(Spanning Tree)는 그래프 이론에서 중요한 개념입니다.
신장 트리는 연결된 무방향 그래프의 모든 노드를 포함하는 부분 그래프로, 사이클이 없는 특성을 가지고 있습니다.
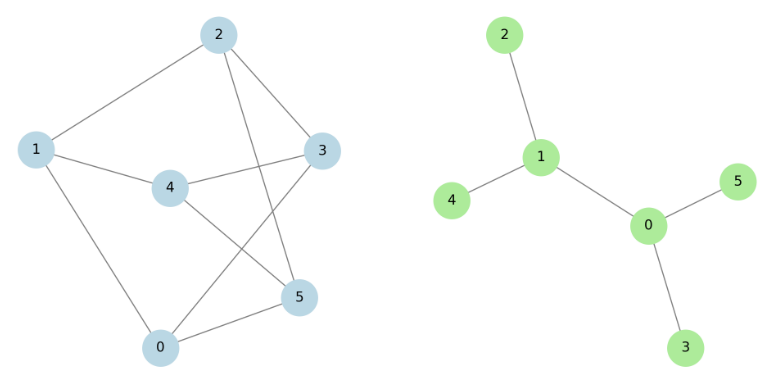
왼쪽 그래프는 원본 그래프를, 오른쪽 그래프는 해당 원본 그래프의 신장 트리(Spanning Tree)를 시각화한 것입니다.
신장 트리는 원본 그래프의 모든 노드를 포함하면서 사이클이 없는 최소의 간선으로 구성된 부분 그래프입니다.
이 경우, 신장 트리는 원본 그래프의 모든 노드를 포함하지만, 원본 그래프보다 적은 수의 간선을 가지고 있으며 사이클이 없습니다.
신장 트리의 주요 특징
1. 모든 노드 포함
신장 트리는 원본 그래프의 모든 노드를 포함합니다. 즉, 원본 그래프의 어떤 노드도 누락되지 않습니다.
2. 최소 연결
신장 트리는 원본 그래프의 노드들을 최소한의 간선으로 연결합니다. 이는 원본 그래프의 연결성은 유지하되, 사이클이 생기지 않도록 간선의 수를 최소화한다는 것을 의미합니다.
3. 사이클 없음
신장 트리에는 사이클이 존재하지 않습니다. 각 노드는 다른 모든 노드와 정확히 하나의 경로로만 연결됩니다.
4. 트리의 성질
신장 트리는 그 이름에서 알 수 있듯이 트리의 특성을 가집니다. 이는 모든 노드가 서로 연결되어 있으며, 사이클이 없고, 부모-자식 관계의 계층 구조를 가지는 것을 의미합니다.
5. 응용 분야
신장 트리는 네트워크 설계, 최소 비용 경로 찾기, 전기 회로 설계 등 다양한 실제 문제를 해결하는 데 사용됩니다. 특히, 최소 신장 트리(Minimum Spanning Tree, MST)는 주어진 그래프 내에서 비용, 길이, 또는 가중치의 합이 최소가 되는 신장 트리를 찾는 문제로, 많은 알고리즘에서 중요한 역할을 합니다.
'개발 > CodingTest' 카테고리의 다른 글
| [이코테] 팀 결성 - 이해까지 도와주는 풀이 (0) | 2024.01.21 |
|---|---|
| [자료구조] 진입차수란? (1) | 2024.01.21 |
| 다양한 알고리즘 - 위상정렬 (0) | 2024.01.21 |
| 신장 트리 - 크루스칼 알고리즘 (0) | 2024.01.19 |
| 다양한 알고리즘 - 서로소 집합을 활용한 사이클 판별 (0) | 2024.01.19 |

