문제
히스토그램에 대해서 알고 있는가? 히스토그램은 아래와 같은 막대그래프를 말한다.
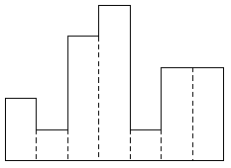
각 칸의 간격은 일정하고, 높이는 어떤 정수로 주어진다. 위 그림의 경우 높이가 각각 2 1 4 5 1 3 3이다.
이러한 히스토그램의 내부에 가장 넓이가 큰 직사각형을 그리려고 한다. 아래 그림의 빗금 친 부분이 그 예이다. 이 직사각형의 밑변은 항상 히스토그램의 아랫변에 평행하게 그려져야 한다.
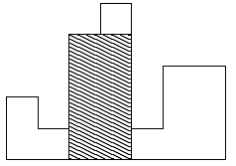
주어진 히스토그램에 대해, 가장 큰 직사각형의 넓이를 구하는 프로그램을 작성하시오.
입력
첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은 자연수 또는 0이다.
출력
첫째 줄에 가장 큰 직사각형의 넓이를 출력한다. 이 값은 20억을 넘지 않는다.
예제 입력
7
2
1
4
5
1
3
3
예제 출력
8
풀이
가장 큰 직사각형의 넓이를 찾기 위한 접근 방식은 스택을 사용하는 것입니다.
1. 히스토그램을 왼쪽에서 오른쪽으로 순회하면서 각 칸의 높이를 고려합니다.
2. 스택을 사용하여 현재까지 확인한 칸들 중에서 직사각형의 후보를 유지합니다. 스택은 높이가 증가하는 순서로 원소를 가지고 있도록 유지됩니다.
3. 현재 칸의 높이가 스택의 맨 위 칸보다 크거나 같으면, 현재 칸을 스택에 추가합니다. 이렇게 하면 현재 위치에서 가능한 직사각형의 왼쪽 끝을 찾는 것입니다.
4. 현재 칸의 높이가 스택의 맨 위 칸보다 작으면, 스택에서 pop하면서 가능한 직사각형을 계산합니다. pop 한 칸은 현재 칸의 오른쪽 끝이 됩니다. 팝한 칸과 스택의 맨 위 칸 사이의 너비를 구하고(인덱스), 이 높이로 가능한 직사각형의 넓이를 계산합니다. 이렇게 하면 가능한 직사각형의 오른쪽 끝을 찾는 것입니다.
5. 이 과정을 반복하면서 가장 큰 직사각형의 넓이를 계산합니다. 스택은 후보 직사각형의 높이가 증가하는 순서로 정렬되므로, 스택에 있는 원소들로 만들 수 있는 직사각형의 넓이를 계산할 수 있습니다.
6. 히스토그램을 모두 순회한 후에도 스택에 남아 있는 칸들이 있다면, 이 칸들을 모두 팝하면서 가능한 직사각형을 계산합니다. 이 때, 각 칸의 높이를 사용하여 직사각형의 넓이를 계산합니다.
이러한 방식으로 스택을 사용하여 히스토그램에서 가장 큰 직사각형의 넓이를 효율적으로 계산할 수 있습니다.
코드에서 사용된 스택과 루프 구조는 이 접근 방식을 구현한 것입니다.
def largestRectangleArea(heights):
stack = [] # 스택을 초기화합니다.
max_area = 0 # 가장 큰 직사각형의 넓이를 초기화합니다.
i = 0 # 인덱스 변수를 초기화합니다.
while i < len(heights):
if not stack or heights[i] >= heights[stack[-1]]:
# 스택이 비어 있거나 현재 칸의 높이가 스택의 맨 위 칸의 높이보다 크거나 같으면
stack.append(i) # 현재 칸의 인덱스를 스택에 추가합니다.
i += 1 # 다음 칸으로 이동합니다.
else:
top = stack.pop() # 스택에서 팝하면서 직사각형을 계산합니다.
width = i if not stack else i - stack[-1] - 1 # 너비를 계산합니다.
max_area = max(max_area, heights[top] * width) # 가장 큰 넓이를 업데이트합니다.
while stack:
top = stack.pop() # 스택에 남아 있는 칸들을 처리합니다.
width = i if not stack else len(heights) - stack[-1] - 1 # 너비를 계산합니다.
max_area = max(max_area, heights[top] * width) # 가장 큰 넓이를 업데이트합니다.
return max_area
# 입력 받기
N = int(input()) # 히스토그램의 가로 칸 수를 입력으로 받습니다.
histogram = []
for _ in range(N):
histogram.append(int(input())) # 각 칸의 높이를 입력으로 받아 히스토그램 리스트에 추가합니다.
# 가장 큰 직사각형의 넓이 구하기
result = largestRectangleArea(histogram)
# 결과 출력
print(result) # 가장 큰 직사각형의 넓이를 출력합니다.
'개발 > CodingTest' 카테고리의 다른 글
| [백준_그래프] 알고리즘 수업 - 너비 우선 탐색 1 (1) | 2024.01.31 |
|---|---|
| [백준_그래프] 24479번 - 알고리즘 수업 - 깊이 우선 탐색 1 (0) | 2024.01.31 |
| [백준_스택2] 17299번 - 오등큰수 (1) | 2024.01.30 |
| [백준_스택2] 17298번 - 오큰수 (2) | 2024.01.30 |
| [백준_스택2] 9935번 - 문자열 폭발 (1) | 2024.01.30 |
